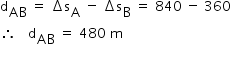Dois veículos, A e B, partem
simultaneamente de uma mesma posição e movem-se no mesmo sentido ao
longo de uma rodovia plana e retilínea durante 120 s. As curvas do
gráfico representam, nesse intervalo de tempo, como variam suas
velocidades escalares em função do tempo.
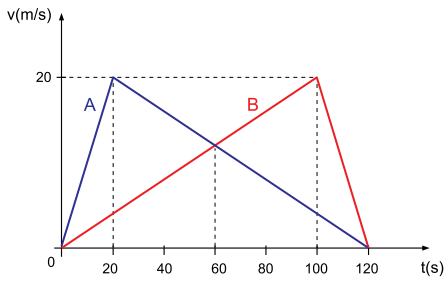
Calcule:
a) o módulo das velocidades escalares médias de A e de B, em m/s, durante os 120 s.
b) a distância entre os veículos, em metros, no instante t = 60 s.
a) O deslocamento dos veículos A e B durante os 120 s pode ser obtido calculando-se a área sob o gráfico v x t fornecido:
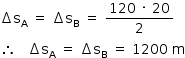
Logo, suas velocidades médias podem ser calculadas de acordo com a definição: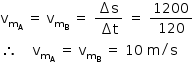
b) O veículo B se desloca em MUV acelerado entre os instantes t = 0 e t = 100 s. Logo, sua aceleração pode ser calculada de acordo com a definição: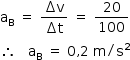
Sendo assim, a velocidade do veículo B no instante t = 60 s pode ser obtida utilizando-se a equação das velocidades: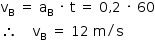
Logo, o deslocamento do veículo B, corresponde à área sob o gráfico v x t, é igual a: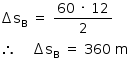
O deslocamento do veículo A, corresponde à área sob o gráfico v x t, é igual a: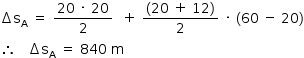
Portanto a distância entre os veículos no instante t = 60 s é igual a: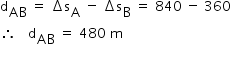
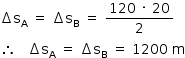
Logo, suas velocidades médias podem ser calculadas de acordo com a definição:
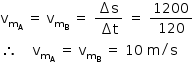
b) O veículo B se desloca em MUV acelerado entre os instantes t = 0 e t = 100 s. Logo, sua aceleração pode ser calculada de acordo com a definição:
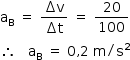
Sendo assim, a velocidade do veículo B no instante t = 60 s pode ser obtida utilizando-se a equação das velocidades:
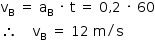
Logo, o deslocamento do veículo B, corresponde à área sob o gráfico v x t, é igual a:
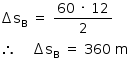
O deslocamento do veículo A, corresponde à área sob o gráfico v x t, é igual a:
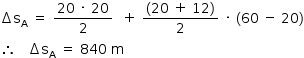
Portanto a distância entre os veículos no instante t = 60 s é igual a: