Um garoto de 40 kg está sentado, em
repouso, dentro de uma caixa de papelão de massa desprezível, no alto de
uma rampa de 10 m de comprimento, conforme a figura.
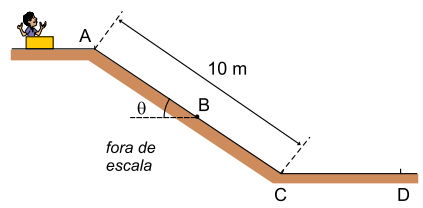
Para que ele desça a rampa, um amigo o empurra,
imprimindo-lhe uma velocidade de 1 m/s no ponto A, com direção paralela à
rampa, a partir de onde ele escorrega, parando ao atingir o ponto D.
Sabendo que o coeficiente de atrito cinético entre a caixa e a
superfície, em todo o percurso AD, é igual a 0,25, que sen θ = 0,6, cos θ
= 0,8, g = 10 m/s2 e que a resistência do ar ao movimento pode ser desprezada, calcule:
a) o módulo da força de atrito, em N, entre a caixa e a rampa no ponto B.
b) a distância percorrida pelo garoto, em metros, desde o ponto A até o ponto D.
Resolução:
a) As forças aplicadas no garoto/caixa no ponto B são:
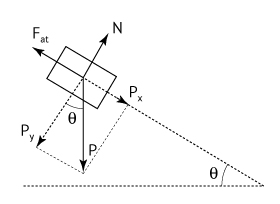
Na direção perpendicular ao plano inclinado, N = Py = Pcos θ.
Dessa forma, a intensidade da força de atrito (Fat):
Fat = µ · N
Fat = 0,25 · 40 · 10 · 0,8 = 80 N.
b) Utilizando-se o plano horizontal de referência em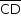 , a energia mecânica em D é nula (o corpo está na referência e com velocidade nula).
, a energia mecânica em D é nula (o corpo está na referência e com velocidade nula).
Em A, há energia potencial gravitacional, que pode ser assim calculada:
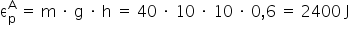
E a energia cinética em A:
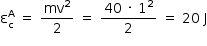
Finalmente, utilizando-se o Teorema da Energia Mecânica:
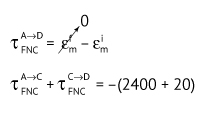
FatA→C · dA→C · cos 180º + FatC→D · dC→D · cos 180º = –2420
80 · 10 · (–1) + 0,25 · 400 · x · (–1) = –2420
–100x = –1620
x = 16,2 m
Assim, o deslocamento de A até D é:
ΔsA→D = ΔsA→C + ΔsC→D
ΔsA→D = 10 + 16,2 = 26,2 m
Resolução:
a) As forças aplicadas no garoto/caixa no ponto B são:

Na direção perpendicular ao plano inclinado, N = Py = Pcos θ.
Dessa forma, a intensidade da força de atrito (Fat):
Fat = µ · N
Fat = 0,25 · 40 · 10 · 0,8 = 80 N.
b) Utilizando-se o plano horizontal de referência em
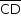 , a energia mecânica em D é nula (o corpo está na referência e com velocidade nula).
, a energia mecânica em D é nula (o corpo está na referência e com velocidade nula).Em A, há energia potencial gravitacional, que pode ser assim calculada:
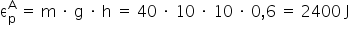
E a energia cinética em A:
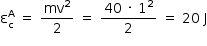
Finalmente, utilizando-se o Teorema da Energia Mecânica:
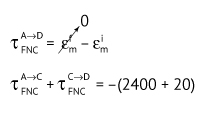
FatA→C · dA→C · cos 180º + FatC→D · dC→D · cos 180º = –2420
80 · 10 · (–1) + 0,25 · 400 · x · (–1) = –2420
–100x = –1620
x = 16,2 m
Assim, o deslocamento de A até D é:
ΔsA→D = ΔsA→C + ΔsC→D
ΔsA→D = 10 + 16,2 = 26,2 m
