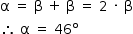Para demonstrar o fenômeno da refração luminosa, um professor faz incidir um feixe monocromático de luz no ponto A da superfície lateral de um cilindro reto constituído de um material homogêneo e transparente, de índice de refração absoluto igual a 1,6 (figura 1).
A figura 2 representa a secção transversal circular desse cilindro, que contém o plano de incidência do feixe de luz. Ao incidir no ponto A, o feixe atravessa o cilindro e emerge no ponto B, sofrendo um desvio angular α.
Sabendo que a velocidade da luz no vácuo é igual a 3 × 108 m/s, que o índice de refração absoluto do ar é igual a 1,0 e adotando sen 53º = 0,8, calcule:
a) a velocidade escalar do feixe luminoso, em m/s, no interior do cilindro.
b) o desvio angular α, em graus, sofrido pelo feixe luminoso ao atravessar o cilindro.
a) Por meio do valor do índice de refração da substância, pode-se determinar a velocidade de propagação da luz no interior desse material.
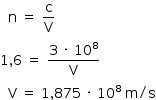
b) A figura a seguir representa a trajetória do raio de luz no interior do cilindro. Note que o triângulo ABO é isósceles. Logo, os ângulos voltados para lados de mesma medida possuem o mesmo valor (θ). Além disso, na primeira refração, o ângulo de incidência é 53o (no ar), e o ângulo de refração é θ (no interior do material). Uma vez que, na segunda refração, o ângulo de incidência é θ (no interior do material), pelo princípio da reversibilidade da trajetória da luz, o ângulo de refração (no ar) deve ser 53o.
No triângulo ABC, o ângulo α é ângulo externo, sendo, portanto, a soma dos dois ângulos internos não adjacentes. Algebricamente:
α = β + β = 2 · β
Assim, para se determinar o desvio angular (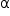
), basta determinar o valor de β.
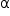), basta determinar o valor de β.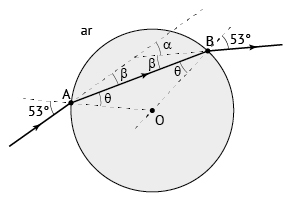
Aplicando a lei de Snell à primeira refração:
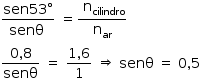
Portanto,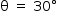 
.
.
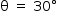A partir da figura:
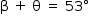
Assim:
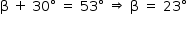
Dessa forma, o desvio angular procurado vale:
