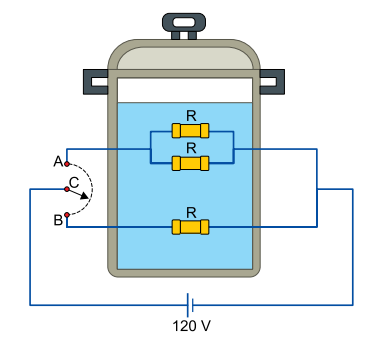
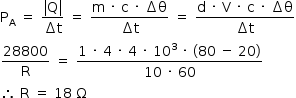A figura representa o esquema de uma panela elétrica, na qual existe uma chave seletora C que pode ser ligada em dois pontos, A e B, que definem qual circuito será utilizado para dissipar, por efeito joule, a energia térmica necessária para o funcionamento da panela.
Uma pessoa deseja utilizar essa panela para elevar a temperatura de quatro litros de água de 20 ºC para 80 ºC. Considerando que o calor específico da água seja 4 × 103 J/(kg · ºC), que a densidade da água seja 1 kg/L, que toda a energia térmica dissipada pelos resistores seja absorvida pela água e, ainda, que a água não perca calor durante o processo, calcule:
a) o valor da razão PA/PB, em que PA e PB são, respectivamente, as potências dissipadas pelos resistores quando a chave C está ligada no ponto A e no ponto B.
b) o valor da resistência elétrica R, em ohms, para que se consiga produzir o aquecimento desejado dessa massa de água, no intervalo de tempo de 10 minutos, com a chave C ligada no ponto A.
a) Com a chave C ligada ao ponto A, tem-se:
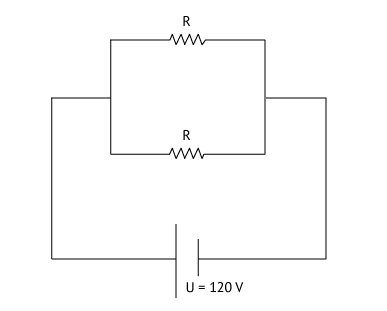
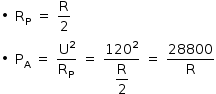
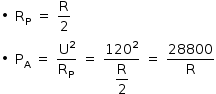
Já com a chave C ligada ao ponto B:
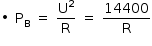
Assim:

b) Como toda a energia térmica dissipada pelos resistores é absorvida pela água: