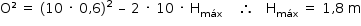Em um jogo de bocha, uma pessoa tem como objetivo atingir uma bola azul parada sobre o solo plano e horizontal. Para isso, ela arremessa obliquamente, a partir do solo, no ponto A, uma bola vermelha, de mesma massa que a azul, com v elocidade inicial v0 = 10 m/s, inclinada de um ângulo de 37º em relação à horizontal, tal que sen 37º = 0,6 e cos 37º = 0,8. Após tocar o solo no ponto B, a bola vermelha pula algumas vezes e, a partir do ponto C, desenvolve um movimento retilíneo, no sentido da bola azul. Imediatamente antes da colisão frontal entre as bolas, a bola vermelha tem velocidade igual a 3 m/s.
Considerando g = 10 m/s², a resistência do ar desprezível e sabendo que, imediatamente após a colisão, a bola azul sai do repouso com uma velocidade igual a 2 m/s, calcule:
a) a velocidade escalar, em m/s, da bola vermelha imediatamente após a colisão com a bola azul.
b) a maior altura h, em metros, atingida pela bola vermelha, em relação ao solo, em sua trajetória parabólica entre os pontos A e B.
a) a velocidade escalar, em m/s, da bola vermelha imediatamente após a colisão com a bola azul.
b) a maior altura h, em metros, atingida pela bola vermelha, em relação ao solo, em sua trajetória parabólica entre os pontos A e B.
a) A situação proposta pode ser representada pelo esquema a seguir:
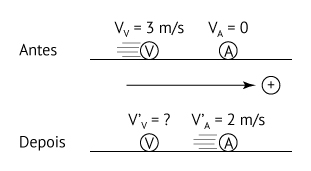
Como o sistema é mecanicamente isolado, tem-se: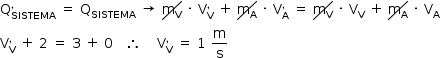
b) Entre os pontos A e B a bola vermelha realiza um lançamento oblíquo. Sendo assim, pode-se utilizar a equação de Torricelli na direção vertical:
V2 = Vo2 + 2 · a · Δs → Vy2 = (Vo · sen 37)2 – 2 · 10 · h
No ponto de altura máxima, Vy = 0: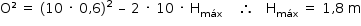
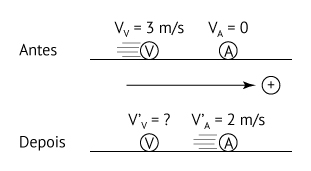
Como o sistema é mecanicamente isolado, tem-se:
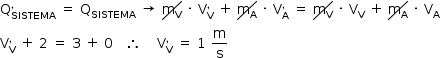
b) Entre os pontos A e B a bola vermelha realiza um lançamento oblíquo. Sendo assim, pode-se utilizar a equação de Torricelli na direção vertical:
V2 = Vo2 + 2 · a · Δs → Vy2 = (Vo · sen 37)2 – 2 · 10 · h
No ponto de altura máxima, Vy = 0: