Considere o triângulo exibido na figura abaixo, com lados de comprimentos a, b e c e ângulos a, β e y.
a) Suponha que a sequência (a, β, y) é uma progressão aritmética (PA). Determine a medida do ângulo β.
b) Suponha que a sequência (a, b, c) é uma progressão geométrica (PG) de razão q = √2. Determine o valor de tan β.
Resolução:
Resolução:
a) Seja r > 0 a razão da P.A. (α, β,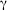 
). Tem-se α = β – r, β e 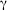= β + r as medidas dos ângulos do triângulo.
Como α + β +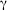 = 180°, tem-se
β – r + β + β + r = 180°
3β = 180°
β = 60°
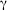). Tem-se α = β – r, β e 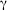= β + r as medidas dos ângulos do triângulo.Como α + β +
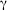= 180°, tem-seβ – r + β + β + r = 180°
3β = 180°
β = 60°
Resposta: a medida do ângulo β é igual a 60°.
b) Como (a, b, c) estão em P.G. de razão q =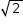 
, então:
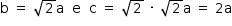
Fica-se com:
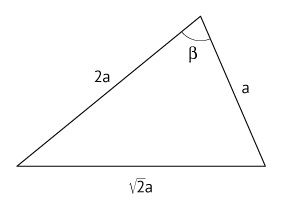
Aplicando o teorema dos cossenos ao triângulo, tem-se:
Como cosβ > 0, tem-se pela relação fundamental:
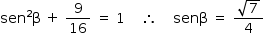
Portanto,
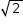, então: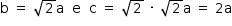Fica-se com:
Aplicando o teorema dos cossenos ao triângulo, tem-se:
Como cosβ > 0, tem-se pela relação fundamental:
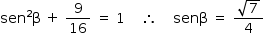
Portanto,
