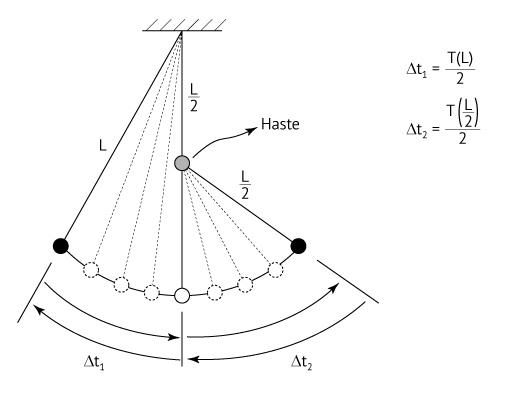
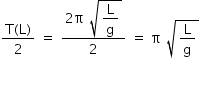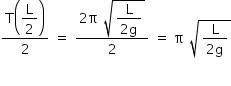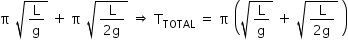Um pêndulo simples, constituído por um fio de comprimento L e uma pequena esfera, é colocado em oscilação. Uma haste horizontal rígida é inserida perpendicularmente ao plano de oscilação desse pêndulo, interceptando o movimento do fio na metade do seu comprimento, quando ele está na direção vertical. A partir desse momento, prove que o período do movimento da esfera é dado por
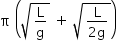
Note e adote:
A aceleração da gravidade é g.
Ignore a massa do fio.
O movimento oscilatório ocorre com ângulos pequenos.