Sofia deveria ter estudado 10 temas de biologia para fazer uma avaliação, porém só estudou 2. Nessa avaliação, ela poderá ser reprovada (R), aprovada com ressalvas (AR) ou aprovada (A). Antes de iniciar a avaliação, a professora de Sofia dá a ela o direito de escolher uma das seguintes estruturas de avaliação:
Avaliação 1 – composta por apenas 2 questões, cada uma tratando de um dos 10 temas (sem repetir os temas), sendo que errar duas implica R, acertar apenas uma implica AR, e acertar as duas implica A.
Avaliação 2 – composta por apenas 3 questões, cada uma tratando de um dos 10 temas (sem repetir os temas), sendo que errar duas ou mais questões implica R, acertar apenas duas implica AR, e acertar as três implica A.
Considere que Sofia sempre acerta questões dos temas que estudou, e que sempre erra questões dos temas que não estudou.
a) Calcule as probabilidades de R, AR e A para o caso de Sofia ter escolhido a avaliação 1.
b) Se Sofia pretende ser aprovada, independentemente de ser com ressalvas (AR) ou diretamente (A), em qual das avaliações ela terá maior chance? Justifique matematicamente sua conclusão por meio de cálculos de probabilidade.
Nas resoluções a seguir, p(X) denota a probabilidade de ocorrer o evento X.
a) A probabilidade de errar as duas questões é dada por 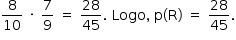
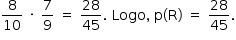
A probabilidade de errar uma questão e acertar a outra é dada por 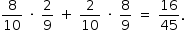
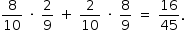
Logo, 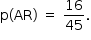
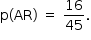
A probabilidade de acertar as duas questões é dada por 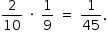
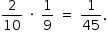
Logo, 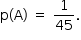
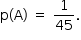
Resposta: 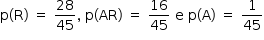
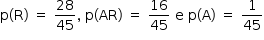
b) Na avaliação 1, p(AR ∪ A) é dada por 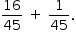
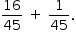
Logo, 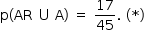
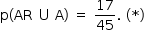
Deve-se calcular, agora, p(AR) e p(A) na avaliação 2.
A probabilidade de acertar duas questões e errar uma é dada por:
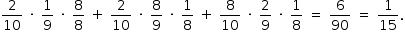
Logo, 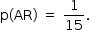
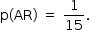
A probabilidade de acertar as três questões é nula, pois, pelo enunciado, Sofia não conseguiria acertar mais que duas questões. Logo, p(A) = 0. Na avaliação 2, p(AR ∪ A) é dada por 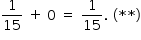
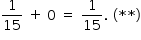
De (*) e (**), conclui-se que a probabilidade de Sofia ser aprovada é maior na avaliação 1.
Resposta: Na avaliação 1.
