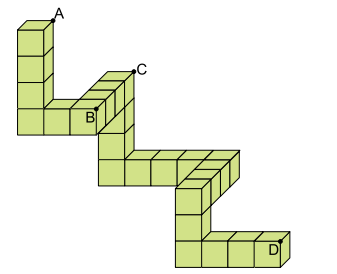
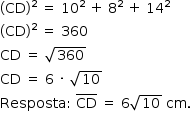Um sólido é formado por 24 cubos idênticos, conforme a figura. O contato entre dois cubos contíguos sempre se dá por meio da sobreposição perfeita entre as faces desses cubos. Na mesma figura também estão marcados A, B, C e D, vértices de quatro cubos que compõem o sólido.
a) Admitindo-se que a medida de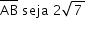 
cm, calcule o volume do sólido.
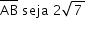cm, calcule o volume do sólido.
b) Calcule a medida de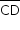 
admitindo-se que a medida da aresta de cada cubo que compõe o sólido seja igual a 2 cm.
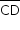admitindo-se que a medida da aresta de cada cubo que compõe o sólido seja igual a 2 cm.
a) Seja ℓ a medida das arestas do cubos. Da figura, tem-se que o segmento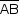 
é uma diagonal de um paralelepípedo reto-retângulo de dimensões ℓ, 2ℓ e 3ℓ, como mostra a figura a seguir:
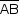é uma diagonal de um paralelepípedo reto-retângulo de dimensões ℓ, 2ℓ e 3ℓ, como mostra a figura a seguir: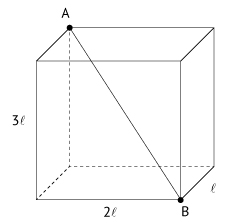
Como AB =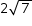 
cm, tem-se:
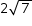cm, tem-se: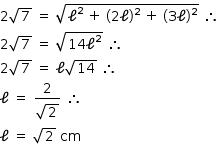
Como o sólido é formado por 24 cubos, cada um de volume ℓ3, esse volume V é:
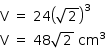
b) Note que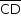 
é uma diagonal de um paralelepípedo reto-retângulo de dimensões 10 cm, 8 cm e 14 cm, como mostra a figura:
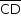é uma diagonal de um paralelepípedo reto-retângulo de dimensões 10 cm, 8 cm e 14 cm, como mostra a figura: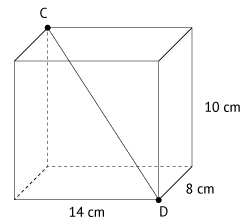
Portanto, tem-se:
