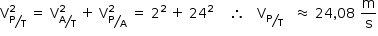Um avião, logo após a aterrissagem, está em movimento retilíneo sobre a pista horizontal, com sua hélice girando com uma frequência constante de 4 Hz.
Considere que em um determinado intervalo de tempo a velocidade escalar desse avião em relação ao solo é constante e igual a 2 m/s, que cada pá da hélice tem 1 m de comprimento e que π = 3. Calcule:
a) a distância, em metros, percorrida pelo avião enquanto sua hélice dá 12 voltas completas.
b) o módulo da velocidade vetorial instantânea, em m/s, de um ponto da extremidade de uma das pás da hélice do avião, em relação ao solo, em determinado instante desse intervalo.
a) Como a frequência da hélice é 4 Hz, isso significa que ela executa 4 voltas a cada segundo. Assim:
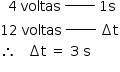
A distância (d) percorrida pelo avião durante esse intervalo de tempo pode assim ser calculada:
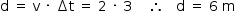
A intensidade da velocidade vetorial instantânea de um ponto P na extremidade de uma das pás da hélice do avião, em relação ao solo, é a mesma em qualquer instante; logo, para obtê-la, podemos analisar a situação dada no enunciado em qualquer instante. Tome-se o instante no qual a hélice se encontra na direção vertical.
Visão Superior
Sendo que:
A velocidade do ponto P em relação ao avião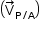 
está associada à rotação da hélice. Logo:
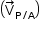está associada à rotação da hélice. Logo: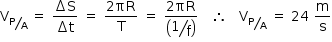
Analisando a figura 1 e utilizando o teorema de Pitágoras;
