(UNIFESP 2016) - QUESTÃO

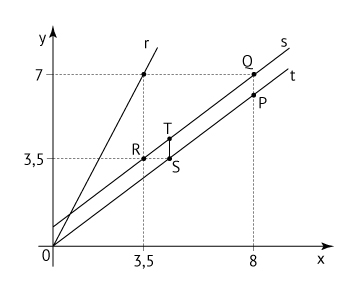
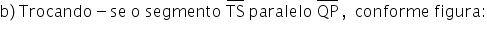Na figura, as retas r, s e t estão em um mesmo plano cartesiano. Sabe-se que r e t passam pela origem desse sistema, e que PQRS é um trapézio.

a) Determine as coordenadas do ponto de intersecção entre as retas r e s.

b) Prove que os lados não paralelos do trapézio PQRS não possuem a mesma medida, ou seja, que o trapézio PQRS não é isósceles.

Resolução:                                                                                                                                    

a) Para obter a intersecção de r e s, devem-se obter as equações de ambas as retas.