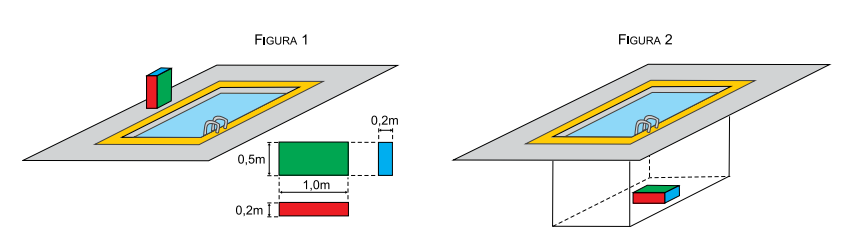
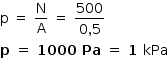Uma caixa de massa 150 kg, com faces
retangulares pintadas nas cores verde, vermelho e azul, está apoiada na
borda plana e horizontal de uma piscina, sobre uma de suas faces azuis,
conforme a figura 1, que também indica as dimensões de cada uma das
faces da caixa. Na situação da figura 2, a caixa está dentro da piscina,
totalmente submersa e apoiada no fundo, em repouso, sobre uma de suas
faces verdes.
Considerando que a água da piscina esteja parada, que sua densidade seja igual a 103 kg/m3 e que g = 10 m/s2, calcule, em pascal:
a) a pressão exercida pela caixa sobre a borda da piscina, na situação indicada na figura 1.
b) a pressão exercida pela caixa no fundo da piscina, na situação indicada na figura 2.
Resolução:
a) As forças que atuam na caixa na situação 1 são o Peso e a Normal.
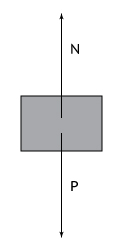
Como o corpo está em equilíbrio: N = P = m . g
Logo: N = 150 · 10 = 1500 N
Assim, a pressão exercida pela caixa sobre o apoio é:
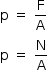
em que a área (A) em contato com a borda da piscina é dada por:
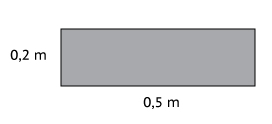
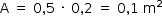
Finalmente:
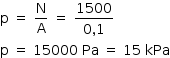
b)
Na figura 2, a caixa está em repouso dentro da piscina. Logo, a resultante das forças é nula.
As forças que atuam na caixa na figura 2 são: Peso (P), Normal (N) e Empuxo (E).
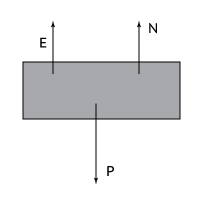
Para que a resultante seja nula:
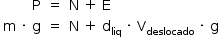
em que
Logo: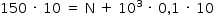
Portanto: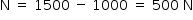
A área em contato com o fundo da piscina é:
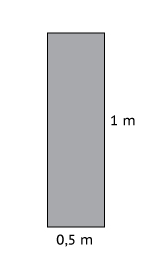
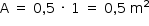
Assim, nessa nova situação, a pressão exercida pela caixa no fundo da piscina será:
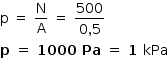
Resolução:
a) As forças que atuam na caixa na situação 1 são o Peso e a Normal.

Como o corpo está em equilíbrio: N = P = m . g
Logo: N = 150 · 10 = 1500 N
Assim, a pressão exercida pela caixa sobre o apoio é:
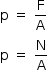
em que a área (A) em contato com a borda da piscina é dada por:

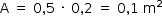
Finalmente:
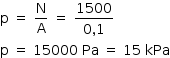
b)
Na figura 2, a caixa está em repouso dentro da piscina. Logo, a resultante das forças é nula.
As forças que atuam na caixa na figura 2 são: Peso (P), Normal (N) e Empuxo (E).

Para que a resultante seja nula:
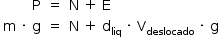
em que
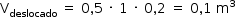
Logo:
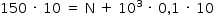
Portanto:
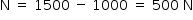
A área em contato com o fundo da piscina é:

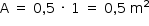
Assim, nessa nova situação, a pressão exercida pela caixa no fundo da piscina será: