A figura mostra uma máquina térmica em que a caldeira funciona como a fonte quente e o condensador como a fonte fria.
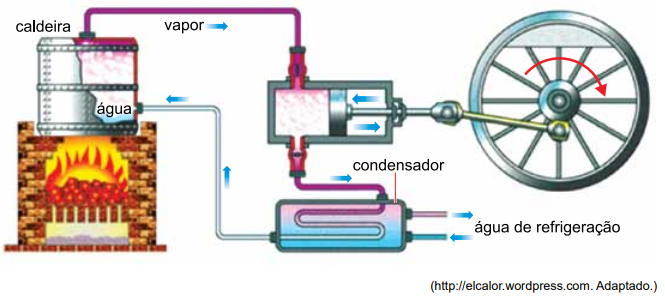
a) Considerando que, a cada minuto, a caldeira fornece, por meio do vapor, uma quantidade de calor igual a 1,6 × 109 J e que o condensador recebe uma quantidade de calor igual a 1,2 × 109 J, calcule o rendimento dessa máquina térmica.
b) Considerando que 6,0 × 103 kg de água de refrigeração fluem pelo condensador a cada minuto, que essa água sai do condensador com temperatura 20 ºC acima da temperatura de entrada e que o calor específico da água é igual a 4,0 × 103 J/(kg⋅ºC), calcule a razão entre a quantidade de calor retirada pela água de refrigeração e a quantidade de calor recebida pelo condensador.
a) O fluxo de energia de uma máquina térmica que opera em ciclos está mostrado a seguir:
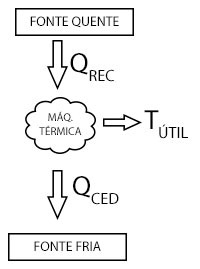
De acordo com o enunciado:
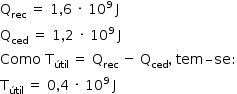
O rendimento de uma máquina térmica é dado por:
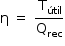
Assim, no caso analisado:
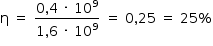
b) A quantidade de calor recebida pelo condensador foi fornecida no enunciado: Qced = 1,2 · 109 J.
A quantidade de calor absorvida pela água da refrigeração é dada por:

A razão pedida é:
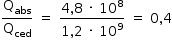

Nenhum comentário:
Postar um comentário