Considere o polinômio cúbico p(x) = x3 − 3x + a, onde a é um número real.
a) No caso em que p(1) = 0, determine os valores de x para os quais a matriz A abaixo não é invertível.
![«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi»A«/mi»«mo»=«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mi»x«/mi»«/mtd»«mtd»«mn»1«/mn»«/mtd»«mtd»«mn»0«/mn»«/mtd»«/mtr»«mtr»«mtd»«mn»0«/mn»«/mtd»«mtd»«mi»x«/mi»«/mtd»«mtd»«mn»1«/mn»«/mtd»«/mtr»«mtr»«mtd»«mi»a«/mi»«/mtd»«mtd»«mn»3«/mn»«/mtd»«mtd»«mi»x«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net//sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=6c854847ba0ec7b2c80611843b6a0383.png)
b) Seja b um número real não nulo e i a unidade imaginária, isto é, i2 = −1. Se o número complexo z = 2 + bi é uma raiz de p(x), determine o valor de |z|.
Resolução:
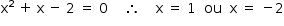
b) Dado que os coeficientes de p(x) são reais, se
é raiz, então 
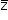também o é. Logo, as três raízes são x1 = 2 + bi, x2 = 2 – bi e x3.
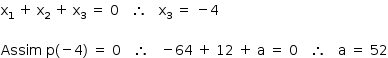
Resolução:
a) A não é invertível ⇔ detA = 0
Assim, A não é invertível se p(x) = 0, dado que p(1) = 0:
Dado que x = 1 é uma raiz, as demais podem ser obtidas por:
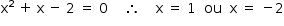
Resposta: x = 1 ou x = –2
b) Dado que os coeficientes de p(x) são reais, se
é raiz, então 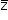também o é. Logo, as três raízes são x1 = 2 + bi, x2 = 2 – bi e x3.
Por Girard, tem-se:
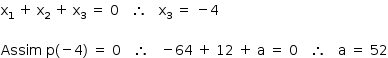
Ainda por Girard:
