O gráfico da parábola dada pela função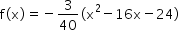 
indica, para uma determinada população de insetos, a relação entre a população total atual (x) e a população total no ano seguinte, que seria f(x). Por exemplo, se a população atual de insetos é de 1 milhão (x = 1), no ano seguinte será de 2,925 milhões, já que f(1) = 2,925.
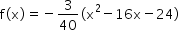indica, para uma determinada população de insetos, a relação entre a população total atual (x) e a população total no ano seguinte, que seria f(x). Por exemplo, se a população atual de insetos é de 1 milhão (x = 1), no ano seguinte será de 2,925 milhões, já que f(1) = 2,925.
Dizemos que uma população de insetos está em tamanho sustentável quando a população total do ano seguinte é maior ou igual a população total atual, o que pode ser identificado graficamente com o auxílio da reta em azul (y = x).
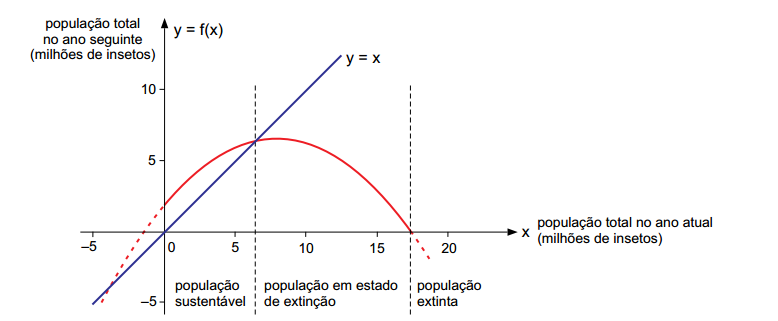
Determine a população total atual de insetos para a qual, no ano seguinte, ela será igual a zero (adote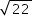 
= 4,7), e determine a população total atual para qual a sustentabilidade é máxima, ou seja, o valor de x para o qual a diferença entre a população do ano seguinte e do ano atual, nessa ordem, é a maior possível.
Resolução:
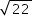= 4,7), e determine a população total atual para qual a sustentabilidade é máxima, ou seja, o valor de x para o qual a diferença entre a população do ano seguinte e do ano atual, nessa ordem, é a maior possível.Resolução:
