A proporção em massa de ouro presente
nas ligas desse metal é geralmente expressa em quilates. Uma peça de
ouro de 24 quilates apresenta 100% do metal em sua composição e
densidade igual a 19,3 g/cm3.
a) Calcule a porcentagem em massa de ouro presente
em uma liga de 18 quilates. Calcule a massa de ouro presente em uma
aliança de massa igual a 5,0 g feita com essa mesma liga.
b) Uma pessoa quis certificar-se da pureza de uma
barra de ouro. Para isso, pesou e mediu as dimensões dessa barra,
obtendo os seguintes valores: massa = 5,8 g ; comprimento = 3,0 cm;
largura = 1,0 cm; altura = 0,1 cm. A partir desses dados, justifique se a
barra analisada era de 24 quilates. Apresente os cálculos efetuados.
a)
24 quilates 100% de ouro
100% de ouro
18 quilates x
x
x = 75% de ouro
5 gramas 100% da massa da aliança
100% da massa da aliança
y 75% é ouro
75% é ouro
y = 3,75 g de ouro na aliança
b)
massa na barra = 5,8 g
volume da barra = 3 cm x 1 cm x 0,1 cm = 0,3 cm3
densidade da barra: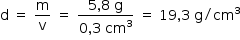
Como a densidade da barra é igual à do ouro, conclui-se que ela é constituída de ouro puro, ou seja, 24 quilates.
24 quilates
 100% de ouro
100% de ouro18 quilates
 x
xx = 75% de ouro
5 gramas
 100% da massa da aliança
100% da massa da aliançay
 75% é ouro
75% é ouroy = 3,75 g de ouro na aliança
b)
massa na barra = 5,8 g
volume da barra = 3 cm x 1 cm x 0,1 cm = 0,3 cm3
densidade da barra:
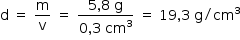
Como a densidade da barra é igual à do ouro, conclui-se que ela é constituída de ouro puro, ou seja, 24 quilates.
