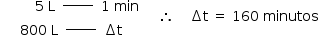Um cilindro de mergulho tem capacidade de 12 L e contém ar comprimido a uma pressão de 200 atm à temperatura de 27 ºC. Acoplado à máscara da mergulhadora, há um regulador que reduz a pressão do ar a 3 atm, para que possa ser aspirado por ela embaixo d’água. Considere o ar dentro do cilindro como um gás ideal, que sua temperatura se mantenha constante e que R = 0,08 atm · L/mol · K.
Considerando que em um mergulho o ar seja aspirado a uma vazão média de 5 L/min, calcule:
a) o número de mols de ar existentes dentro do cilindro no início do mergulho.
b) o tempo de duração, em minutos, do ar dentro do cilindro. Expresse os cálculos efetuados.
a) Considerando-se os dados do enunciado, é possível calcular o número de mols por meio da seguinte equação:
p · V = n · R · T ⇒ 200 · 12 = n · 0,08 · 300
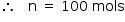
b) Ao escapar do cilindro com temperatura constante, pode-se determinar o volume total do gás:
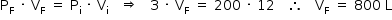
Como a vazão média é de 5 L/min: